The given equation of a line is:
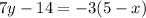
It is required to find the equation of a line that is parallel to this line and passes through the point (-5,5).
Recall that the equation of a line in point-slope form is given as:

Where m is the slope of the line, and the line passes through the point (x₁,y₁).
Rewrite the given equation in the point-slope form:
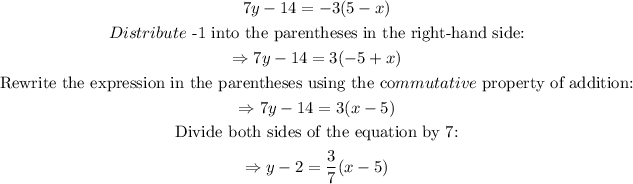
Compare this equation with the standard point-slope form written above, it can be seen that the slope of the line is 3/7.
Recall that the slopes of parallel lines are the same or equal.
It follows that the slope of the required parallel line is also 3/7.
Substitute m=3/7 and the point (x₁,y₁)=(-5,5) into the point-slope form of the equation of a line:
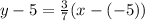
Rewrite the equation in the slope-intercept form and simplify as required:
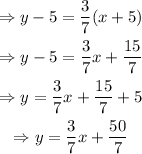
The required equation of the line is y=3/7 x + 50/7.