Solution:
Given:
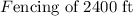
The fenced part of the field must add up to 2400ft.
The possible fencing of the field if the fencing along the river is not needed are shown below;
Possibility 1:
Possibility 2:
From the two possible scenarios, to get the dimensions of the field with the largest area,

Therefore, the dimension of the field with the largest area is 600ft x 1200ft