The given information is:
- The principal P=$7000
- The annual interest rate R is 7%
- The time is T=5 years.
The compounded yearly interest formula is:
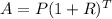
Where A is the amount after T years, P is the principal, R is the interest rate.
If we replace the known values, we obtain:

Now, subtract the principal and find the interest earned:
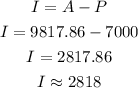
The answer is $2818