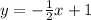Answer:
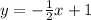
Explanation:
Given the line with the two points:
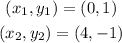
We want to find the equation of the line in the slope-intercept form.
The slope-intercept form is given as:

Step 1: Determine the slope of the line.
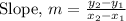
Substitute the given values:
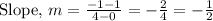
Step 2: Determine the y-intercept.
The line crosses the y-axis at y=1, therefore, the y-intercept, b = 1.
Step 3: Substitute these values into the slope-intercept form.
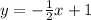
The equation of the line is: