Question

The growth rate of the population of a county isP′(t)=t√(4170t+5430),where t is time in years. How much does the population increase from t=1 year to t=4 years?

Answer 1

If P'(x) is the rate of growth of the population, the actual population is given by the function P(x); therefore, we need to integrate P'(x) as shown below

`P^(\prime)(t)=√(t)(4170t+5430)=t^{(1)/(2)}(4170t+5430)=4170t^{(3)/(2)}+5430t^{(1)/(2)}`

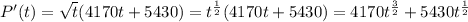
Thus,

`\begin{gathered} \Rightarrow P(t)=\int P^(\prime)(t)dt=\int(4170t^{(3)/(2)}+5430t^{(1)/(2)})dt=4170\int t^{(3)/(2)}dt+5430\int t^{(1)/(2)}dt \\ =4170((2)/(5)t^{(5)/(2)})+5430((2)/(3)t^{(3)/(2)})+C=1668t^{(5)/(2)}+3620t^{(3)/(2)}+C \\ C\rightarrow constant \end{gathered}`

Therefore, calculating the population increase from t=1 to t=4,

`\begin{gathered} \Rightarrow P(4)-P(1)=1668((4)^{(5)/(2)}-(1)^{(5)/(2)})+3620((4)^{(3)/(2)}-(1)^{(3)/(2)})+C-C=1668(31)+3620(7) \\ =77048 \end{gathered}`

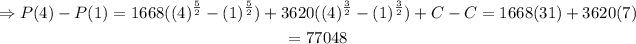
Thus, the answer is 77048