Question

The mass m milligrams of a radioactive substance at time t days, is given by:m(t) = Ae^-ktwhere A and k are constants.The initial mass of the substance is 120 milligrams.The mass of the substance after 10 days is 90 milligrams.a)Sketch the graph to show the relationship between tand mfor ≥ 0 days.b)Show that the value of A is 120.C)Show that the value of & is 0.02877, given to 4 significant figures. d)Using the value of k as 0.02877, find the mass of the substance after 16 days,giving the answer to 3 significant figures.e)Using the value of & as 0.02877, find the day during which the mass of thesubstance first reaches 50 milligrams.

Answer 1

a) Check the graph below, please

b) 120.002

c) 0.02876

d) 75.729g

e) Approximately on the 31st day

1) Considering that the mass is given by this exponential function:

`m(t)=Ae^(-kt)`

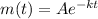
And plugging into that the initial mass, the period, and the final amount of mass:

`90=120e^(-10k)`

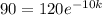
Notice that the initial mass A, is constant and m, is the final amount of mass.

a) Based on that we can plot the following equation:

In this graph, the x-axis represents the days and the y-axis the mass. Since the exponent is negative the graph is like it was reflected across the y-axis.

b) We can demonstrate that the initial value of the mass, A is 120 doing this:

`\begin{gathered} 90=Ae^(-10\cdot0.02877) \\ (90)/(A)=(Ae^(-10\cdot0.02877))/(A) \\ (90)/(A)=e^(-10\cdot0.02877) \\ 90=Ae^(-10\cdot0.02877) \\ A=(90)/(e^(-10\cdot0.02877)) \\ A=120.002\approx120 \end{gathered}`

Note that we have plugged into that the value of k=0.002877 so that we could have just one variable.

c) Plugging into the formula all the variables but k, we have:

`\begin{gathered} 90=120e^(-10k) \\ (90)/(120)=(120e^(-10k))/(120) \\ (3)/(4)=e^(-10k) \\ \ln ((3)/(4))=\ln e^(-10k) \\ -0.2876=-10k \\ k=0.02876\approx0.02877 \end{gathered}`

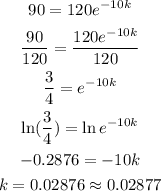
Remember the logarithmic properties so that we could find out k as 0.02877 approximately.

d) Now the point here is the mass "m" in grams for 16 days decaying:

`\begin{gathered} m=120e^(-0.02877\cdot16) \\ m=75.729g \end{gathered}`

Note that we have used the Euler number as 2.718...

e) Similarly let's find it for the time:

`\begin{gathered} 50=120e^(-0.0287\cdot t) \\ (50)/(120)=(120e^(-0.0287\cdot t))/(120) \\ (5)/(12)=e^(-0.0287\cdot t) \\ \ln ((5)/(12))=\ln e^(-0.0287\cdot t) \\ -0.8754=-0.0287t \\ t=30.504\approx31 \end{gathered}`

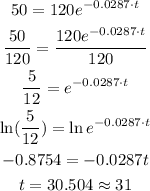
Hence, the mass will reach 50 grams about the 30th to the 31st day