Question

A cyclist rode the first 14-mile portion of his workout at a constant speed. For the 10-mile cooldown portion, of his workout, he reduced his speed by 2 miles per hour. Each portion of the workout took the same time. Find the cyclist's speed during the first portion and find his speed during the cooldown portion.

Answer 1

Step-by-step explanation

To solve the question, we will have to make use of the fact that

`time=(distance)/(speed)`

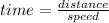
So, we can make the initial speed = v

Thus, we will have the equation:

For the first part

`time=(14)/(v)`

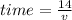
For the second portion, since he reduced the speed by 2miles/hour, the time will be

`time=(10)/(v-2)`

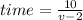
Also, we are told the time for the first and second part of the journey are equal, therefore

`(14)/(v)=(10)/(v-2)`

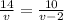
If we solve for v

`\begin{gathered} 14(v-2)=10v \\ 14v-28=10v \\ 14v-10v=28 \\ 4v=28 \\ \\ v=(28)/(4) \\ \\ v=7 \end{gathered}`

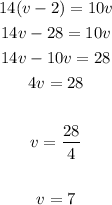
Therefore, the cyclist's speed during the first portion is 7 miles per hour

Also

His speed during the cooldown portion will be (7-2)miles per hour = 5 miles per hour