Answer
![\begin{gathered} \text{ Solution\lparen1\rparen:} \\ (r,\theta)\operatorname{\rightarrow}(1,(\pi)/(2)) \\ \\ \text{Solut}\imaginaryI\text{on}\operatorname{\lparen}2\operatorname{\rparen}: \\ (r,\theta)\operatorname{\rightarrow}(1,-(\pi)/(2)) \end{gathered}]()
Explanation:
We have to find the coordinates of the point of intersection of the two giver curves:
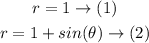
The plot of the equation (1) and (2) is as follows:
The analytical solution backed up by the plot above is as follows:
![\begin{gathered} (1)=(2) \\ \\ 1=1+sin(\theta) \\ 0=sin(\theta) \\ \theta=(\pi)/(2) \\ r=1 \\ \\ \text{ For the following Interval:} \\ 0\leq\theta\leq2\pi \\ \text{ Solution\lparen1\rparen} \\ (r,\theta)\rightarrow(1,(\pi)/(2)) \\ \\ \text{ Solution\lparen2\rparen} \\ (r,\theta)\operatorname{\rightarrow}(1,-(\pi)/(2)) \end{gathered}]()
Screenshot of the answer: