Question

I need help with question 4 and 6. I need to show work also. What I’ve put in is incorrect.The scaling up is applied to the dimensions not the surface area

Answer 1

3) surface area of the box = 162 in²

4) surface area of the box = 16200 in²

6) Volume of the box = 0.104 in³

Step-by-step explanation:

The dimensions of the box:

length = 8in

width = 6 1/2 in = 6.5 in

Height = 2 in

3) surface area of the box = surface area of a rectangular prism

surface area of a rectangular prism = 2(lh + wh + lw)

surface area of a rectangular prism = 2(8 ×2 + 6.5 × 2 + 8 × 6.5)

= 2(16 + 13 + 52)

surface area of a rectangular prism = 2(81) = 162

surface area of the box = 162 in²

4) If the dimensions are scaled up by a factor of 10:

we will multiply each of the initial dimensions by 10. Then we will find the new surface area

length = 8(10) = 80 in

width = 6.5(10) = 65 in

height = 2(10) = 20 in

surface area of the box = 2(lh + wh + lw) = 2lh + 2wh + 2lw

surface area of the box = 2(80)(20) + 2(65)(20) + 2(80)(65)

= 3200 + 2600 + 10400

surface area of the box = 16200 in²

6) Volume of a rectangular prism = l × w × h

initial dimensions: l = 8 in, w = 6.5 in , h = 2 in

Volume of a rectangular prism = volume of the box

Volume of the box = 8 × 6.5 × 2

Volume of the box = 104 in³

The volume we got is the initial/old volume

`\frac{new\text{ volume }}{\text{old volume }}=(scalefactor)^3`
`\begin{gathered} \text{scale factor = 1/10} \\ \frac{new\text{ volume}}{104}\text{ = (}(1)/(10))^3 \\ \text{new volume = 104 }*(1^3)/(10^3)\text{ = 104 }*(1)/(1000) \\ \text{new volume = }(104)/(1000)=0.104in^3 \end{gathered}`

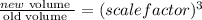
Hence, the volume of the box if it scaled down by a factor of 1/10 is 0.104 in³