Question

21. Two angles are a linear pair. One angle is a fifth the size of the other angle. What are the measurements of the two angles?

Answer 1

Step-by-step explanation

a linear pair of angles must add up to 180 degrees,

Step 1

Let

x= angle1

y= angle2

then

`x+y=180\text{ Equation(1)}`

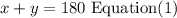
Also

One angle is a fifth the size of the other angle, then

`x=(y)/(5)\text{ Equation (2)}`

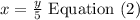
Step 2

replace the value of x from equation(1) in equation(2)

`\begin{gathered} x=(y)/(5) \\ so, \\ (y)/(5)+y=180 \\ (6)/(5)y=180 \\ y=(180\cdot5)/(6) \\ y=150 \end{gathered}`

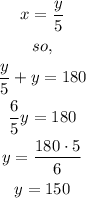
Step 3

replace the value of y=150 in equation (2) to find x

`\begin{gathered} x=(y)/(5) \\ x=(150)/(5) \\ x=30 \end{gathered}`

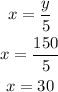
Hence, the answer is 30 and 150