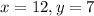Given that the figure is an isosceles trapezoid,
Isosceles trapezoid is a trapezoid whose two opposite sides and two adjacent angles are congruent.
Therefore,
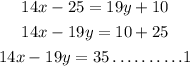
Also,
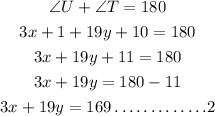
Combining the two equations together and solving for x and y
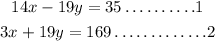
Isolate x from equation 1
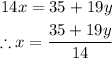
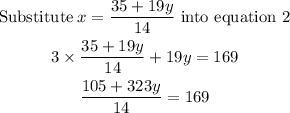
Solve for y
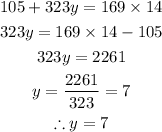
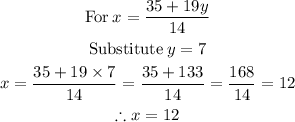
Hence,