The perimeter of the triangle is the sum of the lengths of its sides; therefore, since the side lengths are x, x + 2, and x + 4 cm and the perimeter is 51 cm, we have
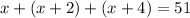
Simplifying the left-hand side of the above gives

subtracting 6 from both sides gives
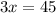
Finally dividing both sides by 3 gives
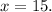
And we have the value of x! We now go on to find the value of the side lengths
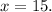
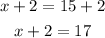

Hence, the side lengths are 15cm, 17cm, and 19cm.