Question

The inequality x/4<=5 has a solution of x=p. write a second inequality that also has a solution of x=p

Answer 1

`(x)/(5)\leq4`

or also;

`(x)/(5)-2\leq2`

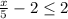
Step-by-step explanation:

Given the inequality;

`(x)/(4)\leq5`

solving the inequality, we have;

multiply both sides by 4;

`\begin{gathered} (x)/(4)*4\leq5*4 \\ x\leq20 \end{gathered}`

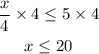
The inequality has a solution of x=p.

So,

`p\leq20`

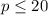
We want to write an inequality that also falls within the range of this solution.

Examples of equations that also have their solution within this range are;

`(x)/(5)\leq4`

also;

`(x)/(5)-2\leq2`

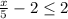
Any of the two inequalities above also has a solution of x=p​.