Question

last month, dory biked 11 times as many miles as karly. together they biked a total of 156 miles. how many miles did dory bike last month? I don’t know if it’s multiplication, division, plus, or minus.

Answer 1

To answer this question we will set and solve a system of equations.

Let d be the number of miles that Dory biked, and k be the number of miles that Karly biked.

Since together they biked a total of 156 miles and Dory biked 11 times as many miles as Karly, then we can set the following system of equations:

`\begin{gathered} d+k=156, \\ d=11k\text{.} \end{gathered}`

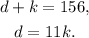
Substituting the second equation in the first one we get:

`11k+k=156.`

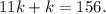
Adding like terms:

`12k=156.`

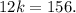
Dividing the above equation by 12 we get:

`\begin{gathered} (12k)/(12)=(156)/(12), \\ k=13. \end{gathered}`

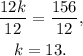
Finally, substituting k=13 in the second equation we get:

`\begin{gathered} d=11\cdot13, \\ d=143. \end{gathered}`

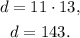
Answer: Dory biked 143 miles.