Question

Which equation best describes the line of best fit?A. Arturo's equation: y = x + 73B. Eleanor's equation: y = -x + 73C. James's equation: y = x + 63D. Kim's equation: y = -x + 63

Answer 1

To find the equation of this line, we need to pick 2 points from the graph:

`\begin{gathered} (x_1,y_1)=(10,60) \\ (x_2,y_2)=(20,50) \end{gathered}`

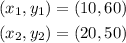
Now, we can use the extended point-slope form of a line to figure the equation of the line shown. The form is given as:

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

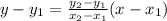
Let's plug in the 2 points we have taken, re-arrange, and find the equation:

`\begin{gathered} y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1) \\ y-60=(50-60)/(20-10)(x-10) \\ y-60=(-10)/(10)(x-10) \\ y-60=-1(x-10) \\ y-60=-x+10 \\ y=-x+10+60 \\ y=-x+70 \end{gathered}`

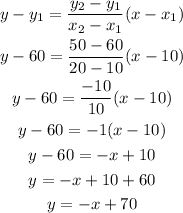
We don't have this exact equation, but the closest is Equation B.

(this discrepancy might be due to the point we chose, they can be a little off from the grid).

Correct Answer

B