Question

Completethefirstmonthoftheamortizationscheduleforafixed-ratemortgage.Themortgageis$106,000,theinterestrateis6.0%,andthetermloanis20years.Findthefollowing:a) TotalPaymentb) InterestPaymentc) PrincipalPaymentd) BalanceofPrincipal

Answer 1

The first step is to calculate the payment, that is going to be equal for each month.

To do that, we apply the annuity equation:

`C=P\cdot((r)/(m))/(1-(1)/((1+(r)/(m))^(n\cdot m)))`

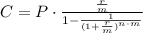
Where C is the total monthly payment, P is the principal (106,000), n is the number of years (20), m is the number of superiods (for monthly payments, is equal to 12) and r is the annual interest rate (6% or 0.06).

Then, we can calculate:

`\begin{gathered} C=106,000\cdot((0.06)/(12))/(1-(1)/((1+(0.06)/(12))^(20\cdot12))) \\ C=106,000\cdot(0.005)/(1-(1)/(1.005^(240))) \\ C=106,000\cdot(0.005)/(1-0.3) \\ C=106,000\cdot(0.005)/(0.7) \\ C=106,000\cdot0.00714 \\ C\approx757.14 \end{gathered}`

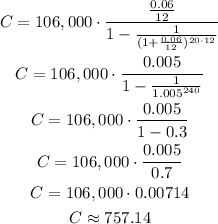
The monthly payment is $757.14.

We can calculate the amount of interest that is paid by applying the simple interest formula:

`I=(r)/(m)\cdot P=(0.06)/(12)\cdot106,000=0.005\cdot106,000=530`

The interest payment is $530, so the difference between the total payment and the interest payment mst be the principal payment U:

`U=C-I=757.14-530=227.14`

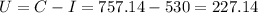
This principal payment is deducted from the principal, so the balance of principal becomes (after the first payment):

`P^(\prime)=P-U=106,000-227.14=105,772.86`

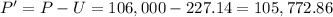
Answer:

a) Total Payment: $757.14

b) Interest Payment: $530.00

c) Principal Payment: $227.14

d) Balance of Principal: $105,772.86