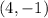Question

Identify the vertex of a quadratic function in standard form? Remember to use x=-b/2ay=2x²-16x+31

Answer 1

Vertex: (4,-1)

Step-by-step explanation:

Given the quadratic function:

`y=2x^2-16x+31`

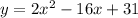
Comparing it with the quadratic function: y=ax²+bx+c

`a=2,b=-16,c=31`

First, determine the x-value of the vertex using the formula: x=-b/2a

`\begin{gathered} x=-(b)/(2a) \\ =-(-16)/(2*2) \\ =(16)/(4) \\ x=4 \end{gathered}`

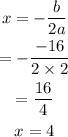
Next, substitute x=4 into y.

`\begin{gathered} y=2x^2-16x+31 \\ =2(4^2)-16(4)+31 \\ =2(16)-64+31 \\ =32-64+31 \\ y=-1 \end{gathered}`

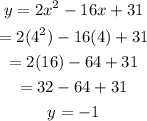
Therefore, the vertex of the function will be:

`(4,-1)`