We need to find the height of the tree. It is represented by x in the following triangle:
Using the Pythagorean Theorem, we have:
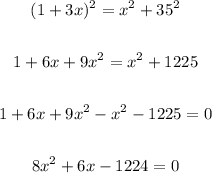
Now, using the quadratic formula, we obtain:
![\begin{gathered} x=\frac{-6\pm\sqrt[]{6^(2)-4(8)(-1224)}}{2(8)} \\ \\ x=\frac{-6\pm\sqrt[]{36+39.168}}{16} \\ \\ x=\frac{-6\pm\sqrt[]{36+39.168}}{16} \\ \\ x=\frac{-6\pm\sqrt[]{39204}}{16} \\ \\ x=(-6\pm198)/(16) \\ \\ x_1=(-6-198)/(16)=(204)/(16)=12.75 \\ \\ x_2=(-6+198)/(16)=(192)/(6)=12 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/u7z1f9h1w7m9bbcsjf10i6iqmhg04d063e.png)
Since x is the height of the tree, it needs to be a positive value. Then, only x₂ is possible.
Therefore, the height of the tree is 12 ft.