Question

Find the distance between the parallel line y = -3x + 4 y = -3x + 1

Answer 1

The distance between the parallel linesy = -3x + 4 and y = -3x + 1 is
`\((√(10))/(3)\)` units.

Step-by-step explanation:

To find the distance between two parallel lines, we can use the formula for the distance d between a point x_0, y_0 and a line Ax + By + C = 0:

`\[ d = (|Ax_0 + By_0 + C|)/(√(A^2 + B^2)) \]`

In this case, the lines y = -3x + 4 andy = -3x + 1 have the same slope, indicating that they are parallel. The formula can be applied with A = 3, B = 1, and C equal to the difference in the y-intercepts, which is 3 units. Plugging these values into the formula, we get
`\(d = (√(10))/(3)\).`

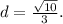
Understanding the formula for the distance between a point and a line is crucial in solving problems involving parallel lines. The numerator in the formula represents the signed distance, and taking the absolute value ensures that we get the distance as a positive value. The denominator involves the coefficients of x and y in the equation of the line, allowing us to calculate the distance accurately.

In conclusion, the distance between the parallel lines y = -3x + 4 and (y = -3x + 1is
`\((√(10))/(3)\)` units. This result provides a quantitative measure of the separation between the two parallel lines in a coordinate plane, demonstrating the application of the distance formula in a geometric context.

Answer 2

EXPLANATION

Given the line:

(1) y= -3x + 4

(2) y = -3x + 1

We can see that the slope is equal to m=-3 in both lines.

We need to start at the y-intercept of the top line, 4. From there, we would go down 3 to reach the line again.

Next, we need to fuse the y-intercept of the bottom line (0,1) and go over 3 to reach the second line. Doing this, we would hit the top line at (0.9,1.3)

We can use these two points in the distance formula to find how far apart the lines are:

`\text{distance}=\sqrt[]{(0.9-0)^2-(1.3-1)^2}`

Subtracting terms:

`\text{distance = }\sqrt[]{(0.9)^2-(0.3)^2}`

Solving the powers:

`\text{distance}=\sqrt[]{0.81-0.09}=\sqrt[]{0.72}=\frac{3\sqrt[]{2}}{5}\approx0.85\text{ units}`

Attaching the graph:

So, the distance between the lines is equal to 0.85 units.