Given:
The diameter of one salt granule is: d = 0.062 mm = 0.0062 cm.
The length of the paper is: l = 28 cm
The width of the paper is: b = 22 cm
To find:
A number of salt grains are needed to cover the paper of the given dimensions.
Step-by-step explanation:
One sand granule when placed on the paper, will cover the area "a" which is given as:
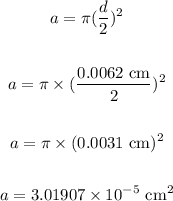
The area "A" of the given paper can be calculated as:
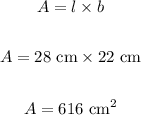
Now, the number of salt grains "N" needed to cover the paper can be calculated as:
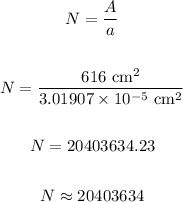
Final answer:
20403634 salt granules are required to cover the area of the given paper.