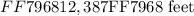Question

1.4.127A mountain with a base 9,538 feet below sea level rises 21,925 feet. What is the elevation above sea level of its peak?

Answer 1

Oceanic mountains are formed from the rocks of sea-bed that rises above the sea-level to its peak height.

We are given that the base of the mountain or the depth underneath the sea-level from where the mountain was formed as:

`\text{depth ( d ) = 9,538 feet}`

The total height/rise of the mountain is given to us as:

`\text{Total height ( H ) = 21,925 feet}`

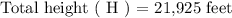
We are to determine the portion of the height that is visible above the sea-level! We know that the mountain base formation starts from below the sea-level at a certain depth ( d ) and the total height ( H ) of the mountain. We can express the portion of height ( h ) that is above sea-level mathematically as follows:

`H\text{ = d + h}`

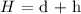
We will plug in the respective values given to us and solve for ( h ):

`\begin{gathered} 21,925\text{ = 9,538 + h} \\ h\text{ = 21,925 - 9,538} \\ \textcolor{#FF7968}{h}\text{\textcolor{#FF7968}{ = 12,387 feet}} \end{gathered}`

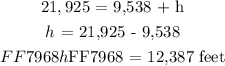
The elevation of mountain above sea-level to its peak height is given as:

`\textcolor{#FF7968}{12,387}\text{\textcolor{#FF7968}{ feet}}`