I need help asap thank you

Question

asked Dec 18, 2023 48.9k views

1 Answer

Takanori · Answer 1 · 2023-12-22T08:03:15+0000

5) Let

be the equation of the parabola that passes through the given points. Then we get that:

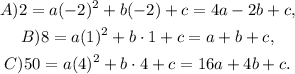
$\begin{gathered} A)2=a(-2)^2+b(-2)+c=4a-2b+c, \\ B)8=a(1)^2+b\cdot1+c=a+b+c, \\ C)50=a(4)^2+b\cdot4+c=16a+4b+c. \end{gathered}$

Subtracting equation B) from equation A) and solving for a we get:

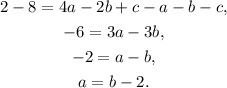
$\begin{gathered} 2-8=4a-2b+c-a-b-c, \\ -6=3a-3b, \\ -2=a-b, \\ a=b-2. \end{gathered}$

Subtracting equation B) from equation C) and solving for a we get:

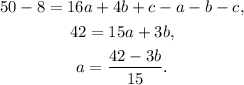
$\begin{gathered} 50-8=16a+4b+c-a-b-c, \\ 42=15a+3b, \\ a=(42-3b)/(15)\text{.} \end{gathered}$

Therefore:

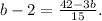
$b-2=(42-3b)/(15)\text{.}$

Solving the above equation for b we get:

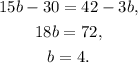
$\begin{gathered} 15b-30=42-3b, \\ 18b=72, \\ b=4. \end{gathered}$

Substituting b=4 in a=b-2 we get:

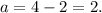
Substituting a=2, b=4 in equation B), and solving for c we get:

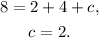
$\begin{gathered} 8=2+4+c, \\ c=2. \end{gathered}$

Answer: Second option.

6) Let