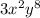For the equation to be an identity, it has to be always true.
Thus, we have to find factors to fill in that will make both sides equivalent for any value of "x".
Since multiplication doesn't depend on the order, we can do it separately for each variable and for the coefficient.
(a)
For the coefficient part, we have 18 in one side and in the other 3. To make they equivalent, we have to multiply the right side by 6, because 3*6 = 18.
Similarly, in the left side we have x^6, and in the right side x^2, so, to make them equivalent, we have to multiply the right side by x^4.
so:
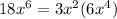
So, the answer to be filled in is:
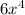
(b) We will do the same thing here.
For the coefficient, we have 40 = 8*__, so we have complete with 5, because 40 = 8*5.
For "x", we have x^2 = x * __, so we are msising one "x", because x^2 = x * x.
For "y", we have y^7 = y^2 * __, so we have to complete it with y^5, because y^7 = y^2 * y^5.
So:
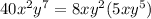
And the answer to fill in:
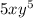
(c)
Here is the same, but since we have positive sign in the left side, and negative in the right, we have to put another negative to cancel it out.
Thus, the coefficient to be completed is 24 = (-3) * (-8).
And the "x" variable, x^6 = x^2 * x^4.
So:
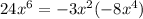
And the answer to fill in:
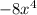
(d)
Same as before, but we have negative sign in both sides, so we don't want to change this, it is already correct. Thus we will use positive sign.
For the coefficient, -48 = -16 * 3.
For "x", x^4 = x^2 * x^2.
For "y", y^10 = y^2 * y^8.
So:
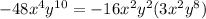
And the answer to fill in: