Question

Line A has a slope of 1 and passes through the points (4, 0) and (-2, -6).Line B passes through the points (1, -1) and (6, 9).Which point below represents where line A intersections line B?A. (-1, -5)B. (0, -4)C. (-2, -4)D. (0, -3)

Answer 1

First, let's find the equation for the line A, using the point-slope form:

`(y-y_1)=m(x-x_1)`

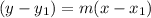
Using the slope m = 1 and the point (x1, y1) = (4, 0), we have:

`\begin{gathered} (y-0)=1(x-4)\\ \\ y=x-4 \end{gathered}`

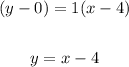
Now, to find the equation for the line 2, let's first calculate the slope, using the two given points in the formula below:

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1)\\ \\ m=(9-(-1))/(6-1)\\ \\ m=(10)/(5)=2 \end{gathered}`

Now, using the point-slope form with the point (1, -1) we have:

`\begin{gathered} (y-(-1))=2(x-1)\\ \\ y+1=2x-2\\ \\ y=2x-3 \end{gathered}`

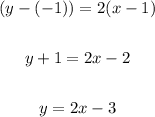
Now, to find the intersection point, let's equate the values of y from each equation:

`\begin{gathered} x-4=2x-3\\ \\ 2x-x=-4+3\\ \\ x=-1\\ \\ \\ y=x-4=-1-4=-5 \end{gathered}`

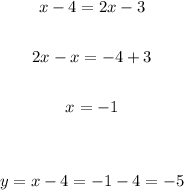
Therefore the intersection point is (-1, -5).

Correct option: A.