For this problem, we are given the coordinates of the endpoint on the diameter of a circle. We need to write the equation in standard form and graph the circle.
To write the equation we need to know the coordinates of the center and the size of the radius. We will first find the center, which is the midpoint of the diameter:
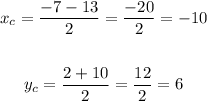
The center is located at (-10, 6). The radius is the distance between the center and one of the given points.
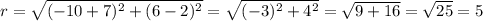
The equation of the circle is:
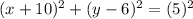
Now we need to graph the circle, we need to find the center (-10,6) and trace the circle in a way that passes through (-7,2) and (-13, 10).