The average force exerted on the bullet can be calculated by using Second Newton Law:
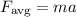
where m is the mass of the bullet and a its acceleration. Consider that acceleration is determined by the following expression (from kinematics):
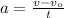
where v is the final speed of the bullet, vo the initial speed and t the time of the change of the velocity.
Then, by replacing the previous expression for a into the formula for Favg, you have:
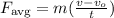
In this case,
m = 0.0100 kg
v = 450m/s
vo = 0m/s (the bullet starts from rest)
t = 1.80ms = 1.80*10^-3 s
Replace the previous values of the parameters into the formula for Favg and simplify:
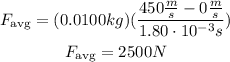
Hence, the average force exerted on the given bullet is 2500N