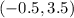Question

the work out to the line x-y+4=0 intersects the curve y=2x^2-4x+1 at points p and q if coordinates of p are 3,7 what are the coordinates of q

Answer 1

Given the equation of a straight line as;

`x-y+4=0`

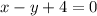
Let's make y the subject of the equation by subtracting (x+4) from both sides of the equation, we have;

`\begin{gathered} x-y+4-x-4=0-(x+4) \\ -y=-(x+4) \\ y=x+4\ldots\ldots\ldots\ldots\ldots\text{.}\mathrm{}\text{equation 1} \end{gathered}`

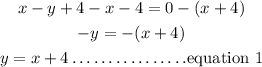
Also, the equation of the curve is;

`y=2x^2-4x+1\ldots\ldots\ldots\ldots\ldots\text{.equation 2}`

Then, we equate equation 1 and equation 2, we have;

`\begin{gathered} x+4=2x^2-4x+1 \\ 2x^2-4x+1-x-4=0 \\ 2x^2-5x-3=0 \\ 2x^2-6x+x-3=0 \\ 2x(x-3)+1(x-3)=0 \\ x-3=0 \\ x=3; \\ 2x+1=0 \\ 2x=-1 \\ x=-(1)/(2) \\ x=-0.5 \end{gathered}`

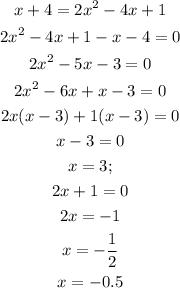
At point x=3;

`\begin{gathered} y=x+4 \\ y=3+4 \\ y=7 \end{gathered}`

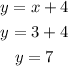
The coordinate of point P is;

`(3,7)`

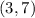
At point x=-0.5;

`\begin{gathered} y=-0.5+4 \\ y=3.5 \end{gathered}`

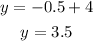
The coordinate of point Q is;

`(-0.5,3.5)`