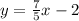Question

write the slope intercept form of the equation of th line trogh the given points.please i have 2 exercise

Answer 1

The equation of a line in slope-intercept form is:

`y=mx+b`

Where m and b are parameters and the solutions to this equation have the form (x,y) and are the points through which the line passes. This means that if we take two points (x,y) we can construct two equations for m and b.

So what we are going to do on each exercise is construct two equations using the one above and the two points given and with those equations we are going to find m and b on each case.

We can start with 8). We have (x,y)=(-5,-5) and (x,y)=(0,-3). Then the equations are:

`\begin{gathered} -5=-5m+b \\ -3=0m+b \end{gathered}`

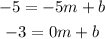
From the second equation we get b=-3. Then we are going to replace b with -3 in the first equation:

`\begin{gathered} -5=-5m+b=-5m-3 \\ -5=-5m-3 \end{gathered}`

Now we add 5m and 5 to both sides of this equation:

`\begin{gathered} -5+5m+5=-5m-3+5m+5 \\ 5m=2 \end{gathered}`

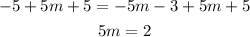
Then we divide both sides by 5:

`\begin{gathered} (5m)/(5)=(2)/(5) \\ m=(2)/(5) \end{gathered}`

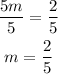
So m=2/5 and b=-3. Then the answer to 8) is:

`y=(2)/(5)x-3`

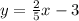
Now for 10) we have (x,y)=(0,-2) and (x,y)=(5,5). Then we have the following equations:

`\begin{gathered} -2=0m+b \\ 5=5m+b \end{gathered}`

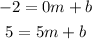
From the first equation we get b=-2. Then we use this value in the second equation:

`\begin{gathered} 5=5m+b=5m-2 \\ 5=5m-2 \end{gathered}`

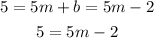
We can add 2 to both sides:

`\begin{gathered} 5+2=5m-2+2 \\ 7=5m \end{gathered}`

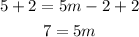
Then we divide both sides by 5:

`\begin{gathered} (7)/(5)=(5m)/(5) \\ (7)/(5)=m \end{gathered}`

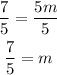
So we have m=7/5 and b=-2. Then the answer to 10) is:

`y=(7)/(5)x-2`