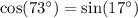Question

PLEASE I REALLY NEED HELP ILL WAIT FOR A QUALITY ANSWER!!!!!!!

Answer 1

At any right angle, the sum of the 2 acute angles is 90 degrees

Then the 2 acute angles are complementary

sin one of the angle = cos the other angle

cos one of the angle = sin the other angle

From the figure, we can see

Triangle UVT is a right angle at V

Then v is the hypotenuse, u and t are the legs od the right angle

Now, let us answer the questions

Part (1):

`\begin{gathered} \sin T=\frac{\text{opposite}}{\text{hypotenuse}} \\ \sin T=(t)/(v) \end{gathered}`
`\begin{gathered} \cos T=\frac{adjacent}{\text{hypotenuse}} \\ \cos T=(u)/(v) \end{gathered}`
`\begin{gathered} \sin U=(opposite)/(hypotenuse) \\ \sin U=(u)/(v) \end{gathered}`
`\begin{gathered} \cos U=\frac{adjacent}{\text{hypotenuse}} \\ \cos U=(t)/(v) \end{gathered}`

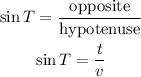
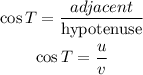
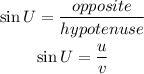
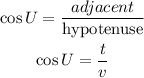
Part (2):

Since
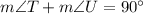`m\angle T+m\angle U=90^(\circ)`complementary

Part (3):

The correct statements are

`\begin{gathered} \cos T=\sin U\rightarrow1st \\ \sin T=\cos U\rightarrow3rd \end{gathered}`

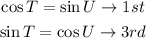
Part (4):

Since cos a= sin b, then

a + b = 90 degrees

To find the missing angle subtract 73 from 90

`90-73=17`

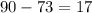
Then the answer is

`\cos (73^(\circ))=\sin (17^(\circ))`