Question

Pythagorean Theorem Digital Escape! Room 3 Can you find the lengths and areas and type the correct code? Please remember to type in ALL CAPS with no spaces. *I need the answer today or I won't be able to get a better grade in math and it is due today. And I need the answers Emmediately.

Answer 1

We are given a right triangle. From each of its sides there are squares. When we have a right triangle of the form:

We can apply the Pythagorean theorem and we get:

`b^2=a^2+c^2`

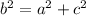
This means that the square of the hypotenuse is equal to the sum of the squares of the sides. Since each square is of the same side of each of the sides of the triangle, this means that the area of the squares is the length of the side squared.

This means that another interpretation of the Pythagorean theorem is that the sum of the areas of the squares form by the sides of the right triangle is equal to the area of the square form by the hypotenuse.

Part 1. To determine the area of "a" we need to notice that "a" is the area of the square formed by the hypothenuse, therefore, its area is the sum of the areas of the squares formed by the sides of the triangles, this means:

`a=9m^2+16m^2=25m^2`

Part 2. Now, we are asked to determine the length of "b". Since "b" is the length of the hypotenuse and "a" is the area of the square formed by the hypotenuse this means that the length of "b" is the square root of "a", this is:

`b=\sqrt[]{a}`

Substituting we get:

`b=\sqrt[]{25m^2}=5m`

Therefore, the length of "b" is 5 meters.