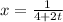Question

Construct parametric equations describing the graph of the following equation.y =2xIf y = 2 + 1, find the parametric equation for x.

Answer 1

Given that,

Given equation is,

`y=(1)/(2x)`

If y=2+t.

To find the parametric equation of x.

Step-by-step explanation:

we know that,

Parametric equation, a type of equation that employs an independent variable called a parameter (often denoted by t) and in which dependent variables are defined as continuous functions of the parameter and are not dependent on another existing variable.

It is given that,

y=2+t

Also we have that,

`y=(1)/(2x)`

Substitute the parametric form of y in the above equation,

we get,

`2+t=(1)/(2x)`

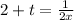
Solve for x, we get

`2x(2+t)=1`
`x(4+2t)=1`
`x=(1)/(4+2t)`

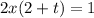
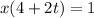
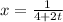
The parametric equation of x is,

`x=(1)/(4+2t)`