Question

Determine the half-life of a radioactive nucleus if 90% of the material has decayed in 366 mins (remember that this means only 10% is remaining).

Answer 1

110 minutes.

Step-by-step explanation:

Let's see the formula of half-life:

`N(t)=N_0\cdot((1)/(2))^{t\text{/h}}.`

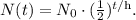
Where N(t) is the quantity remaining, N₀ is the initial quantity, t is time, and h is the half-life.

The problem is telling us that there is 10 % remaining material after 366 minutes. This 10 % corresponds to the division of the quantity remaining and the initial quantity, i.e. N(t)/N₀, so the formula is:

`\begin{gathered} (N(t))/(N_0)=((1)/(2))^{t\text{/h}}, \\ 10\%=((1)/(2))^{t\text{/h}}. \end{gathered}`

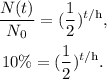
Remember that 10 % in decimals is the same that 0.10:

`0.10=((1)/(2))^{t\text{/h}}.`

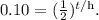
So if we replace the time (in minutes), we will obtain:

`\begin{gathered} 0.10=((1)/(2))^{366\text{/h}}, \\ \log_{(1)/(2)}(0.10)=(366)/(h), \\ h=\frac{366}{\log_{(1)/(2)}(0.10)}, \\ h=110.17\text{ minutes}\approx110\text{ minutes.} \end{gathered}`

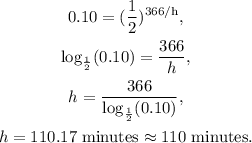
The answer is that the half-life of the radioactive nucleus of the material is 110 minutes.