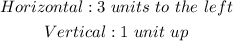Explanation
We are required to identify any horizontal or vertical translations in the given function below:
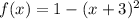
This is achieved thus:
First, the function can be rewritten as:
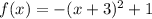
We know that the vertex form of a quadratic function is given as:
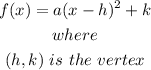
We also know that the following translation rules exist:
Therefore, we can conclude the following on the given function:
• The function reflects on the x-axis.
,
• The function shift 3 units to the left.
,
• The function shifts 1 unit upwards.
Hence, the answers are: