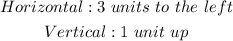Question

For the quadratic function, identify any horizontal or vertical translations. Enter "0" and "none" if there is none.f(x) = 1-(x + 3)² Horizontal:__ units to the (Select an answer (right, left, none)Vertical:__ units to the (Select an answer ( up, down, none)

Answer 1

Explanation

We are required to identify any horizontal or vertical translations in the given function below:

`f(x)=1-(x+3)^2`

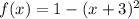
This is achieved thus:

First, the function can be rewritten as:

`f(x)=-(x+3)^2+1`

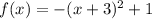
We know that the vertex form of a quadratic function is given as:

`\begin{gathered} f(x)=a(x-h)^2+k \\ where \\ (h,k)\text{ }is\text{ }the\text{ }vertex \end{gathered}`

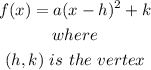
We also know that the following translation rules exist:

Therefore, we can conclude the following on the given function:

• The function reflects on the x-axis.

,

• The function shift 3 units to the left.

,

• The function shifts 1 unit upwards.

Hence, the answers are:

`\begin{gathered} Horizontal:3\text{ }units\text{ }to\text{ }the\text{ }left \\ Vertical:1\text{ }unit\text{ }up \end{gathered}`