Question

Given the equation y = 8sin(pi/6 * x + (7pi)/6) + 4

Answer 1

In general, the sine function can be expressed as shown below

`\begin{gathered} y=Asin(B(x-C))+D \\ A\rightarrow amplitude \\ B\rightarrow period=(2\pi)/(B) \\ C\rightarrow\text{ horizontal shift} \\ D\rightarrow\text{ vertical shift} \end{gathered}`

Then, in our case,

`\begin{gathered} y=8sin((\pi)/(6)x+(7\pi)/(6))+4 \\ \Rightarrow \\ Amplitude=8 \\ Period=(2\pi)/((\pi)/(6)) \\ Horizontal\text{ shift}=-(((7\pi)/(6)))/((\pi)/(6)) \\ Vertical\text{ shift}=4 \end{gathered}`

Simplifying,

`\begin{gathered} \Rightarrow Amplitude=8 \\ Period=12 \\ Horizontal\text{ shift}=-7 \end{gathered}`

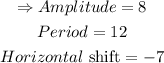
As for the midline, remember that the maximum/minimum of sin(x) is +1/-1; therefore, the midline is

`midline:y=((8+4)+(-8+4))/(2)=(8)/(2)=4`

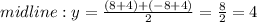
The answers are

Amplitude=8

Period=12

Horizontal shift: 7 units to the left

Midline y=4