Question

The angle of elevation for the hill of a roller coaster is 55 degrees. If the length of the track from the beginning to the highest point is 98 feet, what is the approximate height of the roller coaster when it reaches the top of the first hill?

Answer 1

The base distance between the beginning of the track and the highest point of the roller coaster, the height to the roller-coster, and the distance between the beginning of the track and the highest point form a right triangle.

The distance between the beginning of the track and the highest point, which is 98ft, represents the hypothenuse of the triangle.

The angle of elevation represents one of the acute angles of the right triangle.

We need to find the distance between the floor and the highest point of the roller coaster, which corresponds to the opposite side of the triangle with respect to the angle of elevation.

To find this height you can use the trigonometric ratio sine. This ratio is defined as the quotient between the opposite side to the angle of interest and the hypothenuse:

`\sin \theta=\frac{\text{opposite}}{\text{hypothenuse}}`

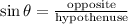
θ corresponds to the angle of elevation

"opposite" corresponds to the measure of the distance to the highest point of the roller coaster

"hypothenuse" corresponds to the distance between the start of the track and the highest point

Replace the expression with the known measures of the angle and the hypothenuse to determine an expression that will allow us to determine the height of the rollercoaster (x)

`\sin 55=(x)/(98)`

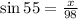
To determine the missing value, x, you have to multiply both sides of the expression by 98

`\begin{gathered} 98\cdot\sin 55=x \\ x=80.28 \end{gathered}`

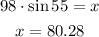
The height of the roller-coaster to its highest point is approximately 80ft