Question

Find the quotient of these complex numbers.(8 - 7i) (4 - 5i) =

Answer 1

Given that

We have to divide the following

`(8-7i)/(4-5i)`

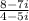
Explanation -

Here we will use the rationalization method in which we will multiply and divide by the denominator by changing the sign in the denominator.

Also we will use the formula a^2 - b^2 = (a+b) (a-b)

In complex numbers i^2 = -1

Then,

`\begin{gathered} (8-7i)/(4-5i)=(8-7i)/(4-5i)*(4+5i)/(4+5i) \\ \\ (8-7i)/(4-5i)=((8-7i)(4+5i))/((4-5i)(4+5i))=(32+40i-28i-35i^2)/(16-(5i)^2) \\ \\ (8-7i)/(4-5i)=(32+12i+35)/(16+25)=(67+12i)/(41)=(67)/(41)+(12)/(41)i \end{gathered}`

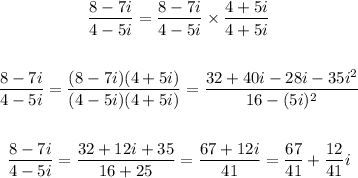
So option D is correct.

Hence the final answer is 67/41 + 12i/41