In this problem, we want to begin the process of elimination without actually solving for the given variables.
The goal is to multiply one of the equations by some constant, and cancel a variable by adding the equations together.
We are given
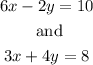
Since we want to eliminate the y-variable, we have to make sure the coefficients are opposites of each other. For example, the opposite of 5 is -5.
We notice the coefficient of y in the first equation is -2, and the coefficient of y in the second equation is 4.
To make them opposites, we need
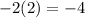
So, we will multiply the first equation by 2:
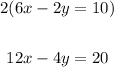
If we add the new equation with the second equation, the y-variable will now cancel:
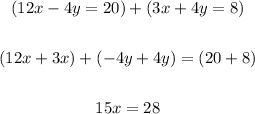
The final answer is to multiply the first equation with 2.