Solution
Step 1:
Draw the diagram to illustrate the information.
Step 2:
Use the Pythagoras theorem to find the height of the pole.
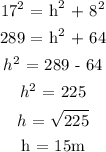
Step 3
b) The height of the second guy wire = d
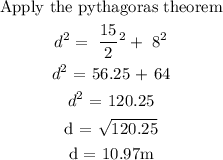
c)

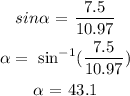
The angle between the two guys' wires = 61.9 - 43.1
Measure of the angle formed between the two wires = 18.8