The correct ratios are
 and
and
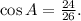 (last option)
(last option)
To find the ratios for sin A and cos A for a right-angled triangle, we can use the definitions of sine and cosine in relation to the sides of the triangle.
The sine of an angle in a right-angled triangle is the ratio of the length of the opposite side to the length of the hypotenuse. The cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse.
The triangle provided in the image is labeled with side lengths: the side opposite angle A is 10 units, the side adjacent to angle A is 24 units, and the hypotenuse (opposite the right angle) is 26 units.
Using these definitions:
-
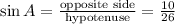
-

These ratios can be simplified by dividing both the numerator and the denominator by the greatest common divisor of each pair of numbers.
Let's simplify these ratios.
The simplified ratios for sin A and cos A are:

