Question

A surveyor wants to find the height of a tower used to transmit cellular phone calls. he stands 120 ft away from the tower and measure the angle of evolution to be 40° . how tall is the Tower?

Answer 1

EXPLANATION

Let's represent the situation on a graph:

Let's call x to the height of the tower.

The height of the tower is given by the following trigonometric relationship:

`\text{tangent 40}=\frac{opposite\text{ cathetus}}{\text{adjacent cathetus}}`

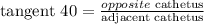
Replacing terms:

`\text{tangent 40 = }(x)/(120)`

Multiplying 120 to both sides:

`120\cdot tangent\text{ 40 = x}`

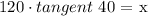
Solving the argument:

`120\cdot0.72=\text{ x}`

Multiplying numbers:

`120\cdot0.72=86.4\text{ ft}`

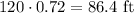
The tower is 86.4 ft tall