Question

Describe the key features of the graph of the quadratic functionf(x) = -5x^2+5.A. Does the parabola open up or down?B. Is the vertex a minimum or a maximum?C. Identify the axis of symmetry, vertex and the y-intercept of the parabola.

Answer 1

The graph of the function will be something like this.

To make the graph correctly we can give values to x to find points in the plane

`\begin{gathered} f(x)=-5x^2+5 \\ x\text f(x) \\ -2|-5(-2)^2+5=-15 \\ -1|-5(-1)^2+5=0 \\ 0|-5(0)^2+5=5 \\ 1|-5(1)^2+5=0 \\ 2|-5(2)^2+5=15 \end{gathered}`

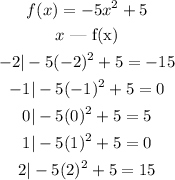
Then the graph passes by the points

`\begin{gathered} (-2,15) \\ (-1,0) \\ (0,5) \\ (1,0) \\ (2,15) \end{gathered}`

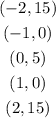
From this, you can draw the points in a cartesian plane.

Once we have the graph we can answer the question.

The parabola open down.

the vertex of the parabola is a maximun since all the other points are below it.

Finally, we see that the axis of symmetry is the y axis. Since the left part of the the graph is the reflection of the right part.

the vertex of the parabola is the point (0,5).

the y intercept of the parabola is 5. we see that from the point (0,5).