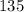
Explanation
Step 1
let
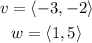
we can use the product scalar formula
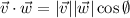
where theta, is the angle between the vectors, so
a) find the measure of the vector v
![\begin{gathered} \lvert\vec{v}\rvert=\sqrt[]{(-3)^2+(-2)^2} \\ \lvert\vec{v}\rvert=\sqrt[]{9+4} \\ \lvert\vec{v}\rvert=√(13) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/vg635hn12sfgc74ywvqbj5dynmwxckubnk.png)
b) now the other vector (w)
![\begin{gathered} \lvert\vec{w}\rvert=\sqrt[]{(1)^2+(5)^2} \\ \lvert\vec{w}\rvert=\sqrt[]{1+25} \\ \lvert\vec{w}\rvert=\sqrt[]{26} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/nlsdv4k87xi0346rt1q3zc3nbyc00bfa6x.png)
Step 2
find the scalar product.
The angle between two vectors can be found using vector multiplication (scalar product)
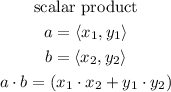
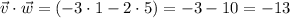
Step 3
Finally, replace in the formula
![\begin{gathered} \vec{v}\cdot\vec{w}=\lvert\vec{v}\rvert\lvert\vec{w}\rvert\cos \emptyset \\ -13=\sqrt[]{13}\sqrt[]{26}\cos \text{ }\emptyset \\ -13=18.38\text{ cos}\emptyset \\ \text{divide both sides by 18.38} \\ (-13)/(18.38)=\frac{18.38\text{ cos}\emptyset}{18.38} \\ -0.07054=\text{ cos }\emptyset \\ \emptyset\text{= }\cos ^(-1)(-0.070) \\ \emptyset=135.01 \\ \text{rounded} \\ \emptyset=135 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/izyamb30oaf5hnixba77ugwbbtzum45ftc.png)
I hope this helps you