Given

Step-by-step explanation
Part A: shorter than 75 in
First we will find the z-score
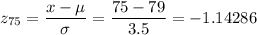
We can then get the P-value from Z-Table:
Answer:
Part B: Between 73 and 83 in

We can then get the P-value from Z-Table for the range 73 to 83
![P\left(-1.71429<p><strong>Answer:</strong></p>[tex]P(73<strong>Part C</strong><p>To solve this, we will find the z score for p(x>z)=7% . Using the z-score calculator.</p>[tex]\begin{gathered} For\text{ }p(x>z)=0.07 \\ z=1.476 \end{gathered}]()
Then we will find the value of x using the z score formula;
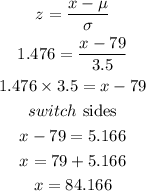
Answer: Approximately 84
Part D
Since a sample of 16 students is now selected, the formula to use will be changed to accommodate the sample.

Therefore, the z score becomes
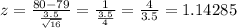
Using the z-score calculator
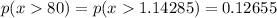
Answer: 0.12655