For this problem we can use the formula for the monthly payment formula given by:
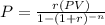
Where:
P= represent the monthly payment (desired value)
PV= Present value = $15999-1700 = $14299
r= rate of interest per period = 0.04/12
n= number of periods = 12* 6 = 72 months
And if we replace into the monthly payment formula we got:
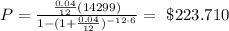
And for this case the monthly payment that she can expect is $223.710