Question

What is the ratio of the area of sector AOB?

Answer 1

C. 1/20

Step-by-step explanation:

The length of AB is calculated as rθ, where r is the radius and θ is the angle.

Then, the given ratio is equal to:

`\frac{length\text{ of AB}}{radius}=(r\theta)/(r)=\theta`

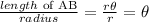
It means that the angle of the sector AOB is θ = π/10

Then, we know that the area of a circle is πr², so for an angle of 2π, the area is πr². Using this, we can calculate the area of the sector with angle π/10 as follows

`\pi/10*(\pi r^2)/(2\pi)=(\pi)/(10)*(\pi r^2)/(2\pi)=(\pi^2r^2)/(20\pi)=(1)/(20)\pi r^2`

Therefore, the ratio of the area of sector AOB to the area of the circle is

`((1/20)\pi r^2)/(\pi r^2)=1/20`

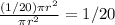
So, the answer is

C. 1/20