Derivatives
The chain rule
Given a f
unction f(x) where x is a function of t, then
f'(t)= f'(x) * x'(t)
When the function to take the derivative from is a composite function, we must use the chain rule.
Let's consider the function in the question
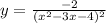
We can manage the expression to make the function easier to take the derivative:
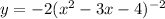
The modified function can be managed as the derivative of the power function: (recall the prime sign ' means derivative).
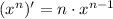
But we can see the expression in parentheses is not x alone, but a function. That is why we must use the chain rule
The expression of the derivative using the chain rule is very similar:
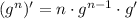
Note the exponent is now applied to a base function g which derivative must be included in the final expression.
Applying the chain rule to the function:
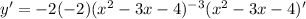
Note the -2 is n, the exponent is now n-1=-3
Now we have to find the remaining derivative. Let's do it apart:
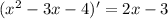
Now, operating in the main derivative, and substituting the above expression:
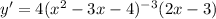
Returning the negative exponent to the denominator:
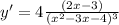
This is the final expression for the derivative
sorry you can't see my answers
hope you soon can see everything in your profile
You are very welcome!
Feel free to let me know how I did by rating our session once you close it