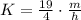We will have the following:
First, we have that the rates for Morgan and Kendall will be the following (Respectively):
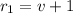
&
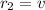
And the distance will be given by:
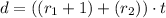
Here "t" is the time.
Now, we replace the values and solve for the rate "v":
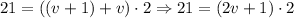
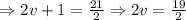
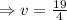
So, Morgan and Kendall's rates are respectively:
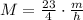
&