Answer:
The dialation is of -(1/9)
Explanation:
I will write a matrix for the triangle before dialation. It is:
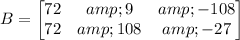
The matrix after the dailation is:
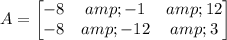
The relationship between the matrix is:
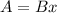
In which x is the dilation.
So
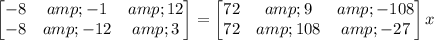
Taking two elements at the same position, i will take the first ones:
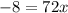
Now we find the dilation x.
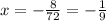
The dialation is of -(1/9)