Question

Please help me with parts 2 and 3 of this Honors Precalc problem.

Answer 1

The Moivre's theorem can be used to find roots of complex numbers. Given a complex number:

`z=r(\cos(\theta)+i\sin(\theta))`

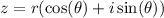
Then, the theorem says, to find the n-th root:

`\sqrt[n]{z}=\sqrt[n]{r}(\cos((\theta+2\pi k)/(n))+i\sin((\theta+2\pi k)/(n)))`

Where n and k are natural numbers. The argument of the sine and cosine functions is the angle of the roots, the n-th root of the module is the module of the n-th root of the complex number.

Thus, to find the fourth root, n =4:

`\sqrt[4]{z}=\sqrt[4]{r}(\cos((\theta)/(4))+i\sin((\theta)/(4)))`

Since in step 1 the polar form of the number is written, we can write the formula for the 4-th roots:

`\sqrt[4]{z}=\sqrt[4]{2}(\cos(((\pi)/(3)+2\pi k)/(4))+i\sin(((\pi)/(3)+2\pi k)/(4)))=\sqrt[4]{2}(\cos((\pi)/(12)+(\pi k)/(2))+i\sin((\pi)/(12)+(\pi k)/(2))`

Thus:

`Module=\sqrt[4]{2}`

And the angles are:

`\begin{gathered} k=0\Rightarrow(\pi)/(12)+(\pi\cdot0)/(2)=(\pi)/(12)\frac{}{} \\ . \\ k=1\Rightarrow(\pi)/(12)+(\pi\cdot1)/(2)=(7\pi)/(12) \\ . \\ k=2\Rightarrow(\pi)/(12)+(\pi\cdot2)/(2)=(13\pi)/(12) \\ . \\ k=3\Rightarrow(\pi)/(12)+(\pi\cdot3)/(2)=(19\pi)/(12) \end{gathered}`

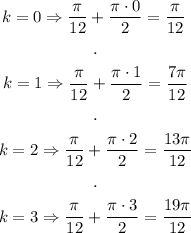
Those are the angles of the fourth roots.

Next, for part 3, we can put all this together to write the roots in polar form:

`\begin{gathered} z_1=\sqrt[4]{2}(\cos((\pi)/(12))+i\sin((\pi)/(12))) \\ . \\ z_2=\sqrt[4]{2}(\cos((7\pi)/(12))+i\sin((7\pi)/(12))) \\ . \\ z_3=\sqrt[4]{2}(\cos((13\pi)/(12))+i\sin((13\pi)/(12))) \\ . \\ z_4=\sqrt[4]{2}(\cos((19\pi)/(12))+i\sin((19\pi)/(12))) \end{gathered}`